বাইনারি সার্চ ট্রি এর প্রতিটি নোডে একটি করে মান থাকে। এখানে মান গুলো এমন ভাবে থাকে যেন, ট্রি এর লেফট সাবট্রি (Left subtree) এর সকল মান রুট নোডে থাকা মান থেকে ছোট হয়, আর রাইট সাবট্রি (Right subtree) এর সকল মান রুট নোডের মান থেকে বড় হয়।
নিচে একটি চিত্রের মাধ্যমে একটি বাইনারি সার্চ ট্রি বোঝানোর চেস্টা করেছি। চিত্রটি খেয়াল করলে দেখবে যে, রুট নোডে আছে ২৫, আর এর বামের সাবট্রি গুলোর মান এই ২৫, মানে রুট নোডের মান থেকে ছোট আছে। আবার ডান দিকের সাবট্রি গুলোর মান রুট নোড এর মান ২৫ থেকে বড় আছে। অর্থাৎ কোনো নোডের বাম দিকের সব মান ঐ নোডের মান থেকে ছোট, আর ডান দিকের সব মান বড়।
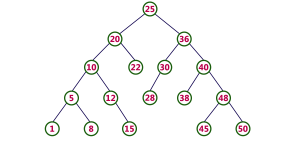
আমরা লিংকড লিস্টের মতো করে বাইনারি সার্চ ট্রি বানাতে পারি। সেক্ষেত্রে প্রতিটি নোডে আমাদের দুটি লিংকের দরকার হবে, একোটি লেফট চাইল্ড এর জন্য, অপরটি রাইট চাইল্ডের জন্য। অনেক সময় প্যারেন্ট এর জন্যও আলাদা লিঙ্ক রাখতে হয়।
একোটি বাইনারি সার্চ ট্রিতে কোন একটি সংখ্যা আছে কি না, তা খুজে বের করা খুব সহজ। তুমি কোন একটি নোডে গিয়ে দেখবে যে তুমি যেই সংখ্যা খুজছো তা এখানে থাকা সংখার থেকে ছোট না বড়। যদি সমান হয় তাহলে তো পেয়েই গেলে, আর যদি ছোট হয় তাহলে বাম দিকে যাবে আর বড় হলে ডান দিকে যাবা। এরকম করে তুমি চাইলে ইনসার্টও করতে পারবে, যদিও ডিলেট করা একটু কঠিন।
সত্য বলতে, অনেক সময় প্রোগ্রামিং প্রতিযোগিতায় আমরা সত্যিকার ভাবে ডিলেট না করে প্রতিটি নোডে একটি করে ফ্লাগ রাখি। ডিলেট করতে চাইলে সেই ফ্লাগ কে বন্ধ করে দিলেই হয়।
এখন কথা হচ্ছে, একটি অ্যারেতে সংখ্যা না রেখে, আমরা এইরকম ট্রি আকারে সংখ্যা রাখলে লাভ কি? একটু ভালো করে খেয়াল করো, একটি সংখ্যা খোজার সময় আমরা যখন একোটি নোডে থাকা সংখার সাথে আমাদের সংখ্যা, মানে যেটা খুজছি, তার তুলনা করি, তখন সেই তুলনার ভিত্তিতে আমরা একদিক বাদ দিয়ে আরেক দিকে যেতে পারি। এখন এই ভাগাভাগি যদি ঠিক অর্ধেক হয়, তাহলে আমরা প্রতিবার অর্ধেক সংখ্যা বাদ দিতে পারি। ঠিক বাইনারি সার্চের মত। তাহলে আমরা যদি ঠিক অর্ধেক অর্ধেক করে রাখতে পারি, তাহলে আমরা O(logn) এই সার্চ করতে পারবো।
আবার ঝামেলা, তাহলে আমাদের বাইনারি সার্চের সঙ্গে বাইনারি সার্চ ট্রি এর পার্থক্য কোথায় ? আচ্ছা, বাইনারি সার্চে আমরা কোন একোটি সংখাকে ইনসার্ট বা ডিলিট করতে পারি না, কিন্তু বাইনারি সার্চ ট্রিতে ইনসার্ট বা ডিলিট দুটো কাজই করতে পারি।
একটু ভাবলে বুঝবে যে সাধারণভাবে সংখ্যাগুলোকে ইনসার্ট করালে কিন্তু আমাদের BST অনেক লম্বা হয় যেতে পারে, যেমন ১ এর ডানে ২, ২ এর ডানে ৩ এরকম করে n পর্যন্ত যদি সংখ্যা থাকে, তাহলে কিন্তু O(n) সময় লেগে যাবে। এইধনের সমস্যা যাতে না হয়, সেজন্য আমাদের BST কে ব্যালান্স করে নিতে হয়, যেন ট্রি এর উচ্চতা বেশি বড় না হয়।
এইধনের আরো কিছু ডেটা স্ট্র্যাকচার আছে, যেমন এভিএল ট্রি (AVL Tree), রেড ব্ল্যাক ট্রি (Red Black tree), ট্রেপ (Treap), স্প্লে ট্রি (Splay Tree) ইত্যাদি। তোমরা চাইলে এসব বিষয়ে ইন্টারনেটে খুজে দেখতে পারো। তবে বেশির ভাগ সময় আমরা STL এর ম্যাপ বা সেট ব্যবহার করে BST সংক্রান্ত অনেক কাজ করে ফেলতে পারি।
এখনো যদি তুমি বাইনারি সার্চ ট্রি বুঝতে না পারো, তবে নিচের কোড গুলো একটি ভালো করে বোঝার চেস্টা করো, দেখবে এতক্ষণ যা বলেছি তা ছবির মত চোখের সামনে ভাসছে।
সি দিয়ে বাইনারি সার্চ ট্রি ইমপ্লিমেন্টশনঃ
// C function to search a given key in a given BST
struct node* search(struct node* root, int key)
{
// Base Cases: root is null or key is present at root
if (root == NULL || root->key == key)
return root;
// Key is greater than root's key
if (root->key < key)
return search(root->right, key);
// Key is smaller than root's key
return search(root->left, key);
}
পাইথন দিয়ে বাইনারি সার্চ ট্রি ইমপ্লিমেন্টশনঃ
# A utility function to search a given key in BST
def search(root,key):
# Base Cases: root is null or key is present at root
if root is None or root.val == key:
return root
# Key is greater than root's key
if root.val < key:
return search(root.right,key)
# Key is smaller than root's key
return search(root.left,key)
জাভাস্ক্রিপ্ট দিয়ে বাইনারি সার্চ ট্রি ইমপ্লিমেন্টশনঃ
class Node {
constructor(value) {
this.value = value;
this.right = null;
this.left = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
//inserts a number into the tree. Returns the entire tree.
insert(value) {
const newNode = new Node(value);
if (!this.root) {
this.root = newNode;
return this;
}
let current = this.root;
const rnLoop = true;
while (rnLoop) {
if (value === current.value) return undefined;
if (value < current.value) {
if (!current.left) {
current.left = newNode;
return this;
}
current = current.left;
} else {
if (!current.right) {
current.right = newNode;
return this;
}
current = current.right;
}
}
}
//finds the given number and returns it. If its not found, returns `null` or `undefined`.
find(value) {
if (!this.root) return null;
let current = this.root;
const rnLoop = true;
while (rnLoop) {
if (!current) return undefined;
if (value === current.value) return current;
if (value < current.value) {
current = current.left;
} else {
current = current.right;
}
}
}
//checks if a given number exists in the tree. If its in the tree, returns `true`, otherwise `false`
contains(value) {
if (!this.root) return null;
let current = this.root;
const rnLoop = true;
while (rnLoop) {
if (!current) return false;
if (value === current.value) return true;
if (value < current.value) {
current = current.left;
} else {
current = current.right;
}
}
}
}
//EXAMPLES==================================================================================
const binarySearchTree = new BinarySearchTree();
binarySearchTree.insert(10); //returns the entire list
binarySearchTree.insert(6); //returns the entire list
binarySearchTree.insert(2);
binarySearchTree.insert(20);
binarySearchTree.insert(34);
binarySearchTree.insert(69);
binarySearchTree.insert(4);
binarySearchTree.find(4); //returns `Node {value: 2, right: Node, left: null}`
binarySearchTree.find(20);
binarySearchTree.find(123); //returns `undefined`
binarySearchTree.contains(6); //returns `true`
binarySearchTree.contains(123); //returns `false`
আশাকরি বাইনারি সার্চ ট্রি সম্পর্কে তোমার আর কোন প্রশ্ন নেই, যদি থেকে থাকে তবে আমাকে জিজ্ঞেস করতে পারো। তবে হ্যা, আমি শুধু বাইনারি সার্চ ট্রি নিয়ে কথা বলেছি, তোমাকে কিন্তু শিখতে হবে কিভাবে ইনসার্ট করতে হয়, বা কিভাবে ডিলেট করতে হয়।
